probability
Tags: statistics
- https://www.vfu.bg/en/e-Learning/Math--Bertsekas_Tsitsiklis_Introduction_to_probability.pdf
- https://realnotcomplex.com/probability-and-statistics/probability-theory/introduction-to-probability-by-dimitri-p-bertsekas-and-john-n-tsitsiklis
- https://realnotcomplex.com/probability-and-statistics/probability-theory/a-short-introduction-to-probability-by-dirk-p-kroese
- https://faculty.math.illinois.edu/~r-ash/BPT.html
- https://realnotcomplex.com/probability-and-statistics/probability-theory/basic-probability-theory-by-robert-b-ash
- https://realnotcomplex.com/
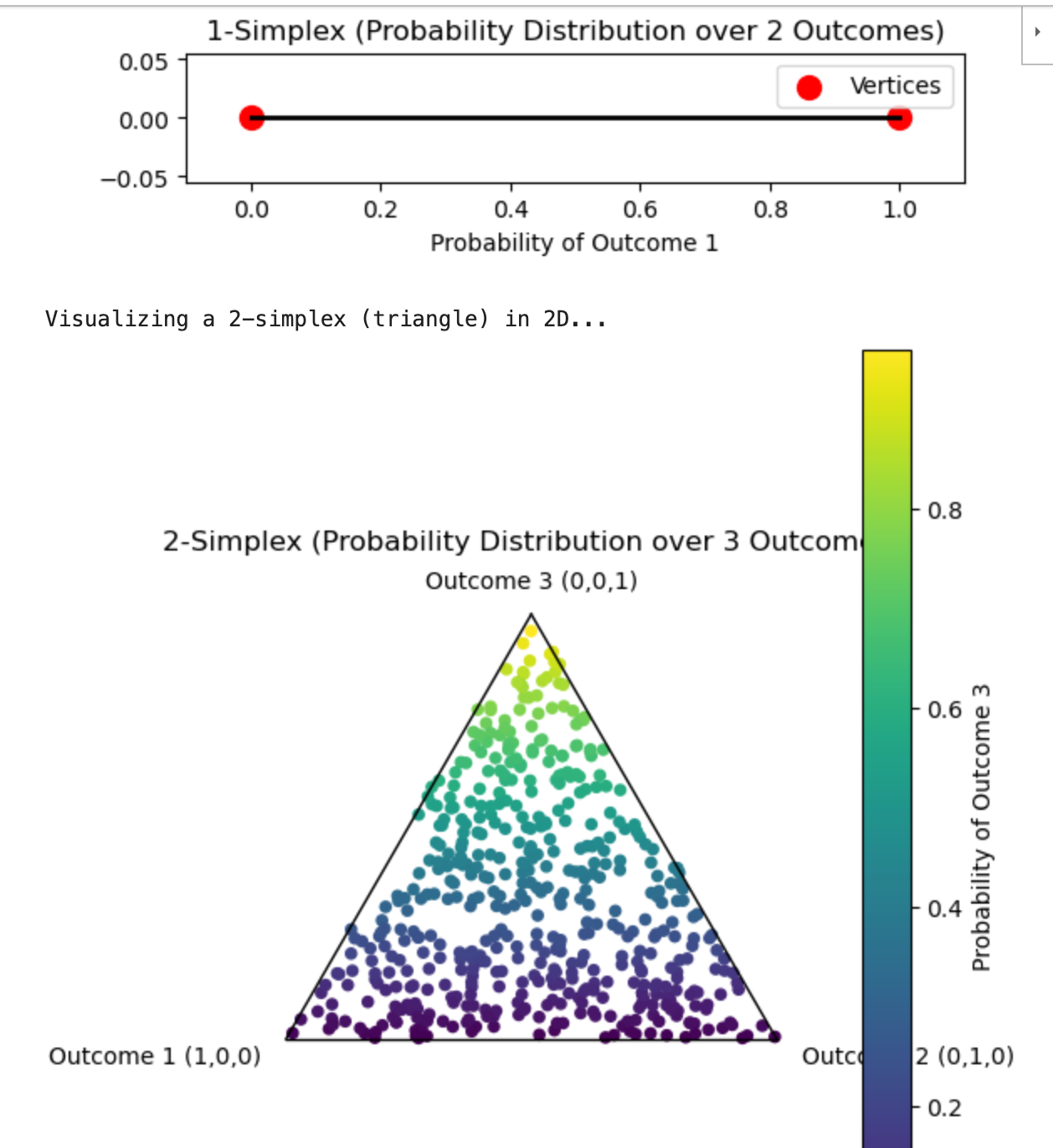
Probability Simplex
- A shape where each vertex represents a probability
- Example:
Outcomes: {1, 2, 3}
Let the probabilities be p1,p2,p3.
We know that p1≥0, p2≥0, p3≥0, and p1+p2+p3=1.
Geometrically, this can be represented by a 2-simplex, which is an equilateral triangle.
Each vertex of the triangle represents a distribution where one outcome has a probability of 1 and the others have a probability of 0.
Vertex 1: p1=1,p2=0,p3=0
Vertex 2: p1=0,p2=1,p3=0
Vertex 3: p1=0,p2=0,p3=1
Any point inside the triangle (or on its edges) represents a probability distribution where p1,p2, and p3 are non-negative and sum to 1. The closer a point is to a vertex, the higher the probability of that corresponding outcome.